Markov Decision Process

What is it?

The Markov Decision Process (MDP) is a mathematical decision-making model widely used in Probability and Reinforcement Learning to determine the best policy of an agent, which is the strategy that maximizes rewards over time. MDP assumes a stochastic process that satisfies the Markov Property.

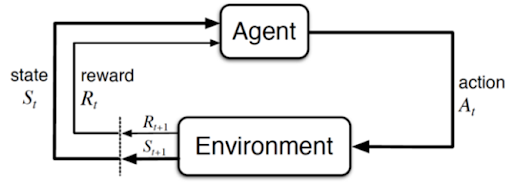
The Markov Process is normally used in discrete action spaces, with which its finite set of actions and spaces, categorizes a Markov Chain.

---

How does it work?

An agent in a Markov Decision Process always tries to find the optimal policy ${\pi }^{\ast }$, which is the the rule for choosing the actions, maximizing rewards over time by using value functions to estimate the expected reward. However, discounts factors are added into the equation to prevent an infinite policy, which can also weigh some rewards, making it more valuable than others and can also make the agent pursue short or long term rewards.

To calculate the expected return, starting from a state $s$ and a policy $\pi$, also called value or utility function:

$$V^{\pi }(s)={\mathbb{E}}_{\pi }\left[\sum _{t=0}^{\infty }{\gamma }^{t}R(S_t)\right]$$

The optimal policy ${\pi }^{\ast }$ is obtained with the highest $V^{\pi }(s)$, which can be denoted as:

$$V^{\ast }(s)=ma{x}_{\pi }{V}^{\pi }(s)$$

However, it’s a very expensive solution. To discover the optimal values, Richard Bellman proposed an iterative method, which is named Dynamic Programming.