Balanced Binary Trees

What is it?

A balanced binary tree, also known as the Adelson-Veslky & Landis tree, is a algorithm applied to a Binary Tree data structure, which creates a specific case of a Binary Tree. It inherits all properties of a Binary Search Tree, and it tries to optimize the performance of searching through the tree by balancing its nodes, avoiding long subtrees and creating more wider trees.

---

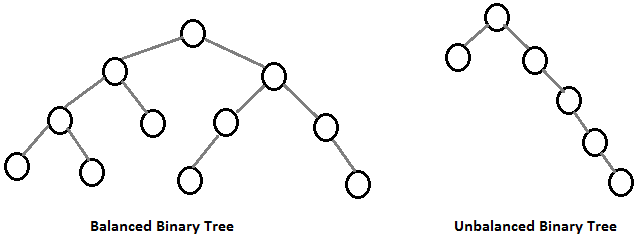
How does it work?

While the balanced binary tree inherits all properties from a binary search tree, it adds balancing, which states that the difference of height between the right subtree and the left subtree should be always equal to $0$, $1$, or $-1$. In other words, the height difference should be less than $2$.

The algorithm to check balancing, should be applied to all nodes of the tree, as it follows:

• Calculate the relative height of the right subtree

  Count how many levels are in between the desired node and the deepest leaf node of the right subtree. In others words, calculate the height of it.

• Calculate the relative height of the left subtree

  Apply the same procedure, but now to the left subtree of the desired node.

• Calculate the height difference

  Calculate the difference between the numbers from the first and second step. The result should be $-1\le x\le 1$. If it is, the desired node is balanced. If not, the tree is imbalanced, and should the node should be balanced.