Linear Transformations

What is it?

In Linear Algebra, linear transformations (or linear map) are functions which linearly transforms matrices and arrays to different Vector Spaces. They are widely used in graphical computing to transform graphics and engineering to work with different physical structures.

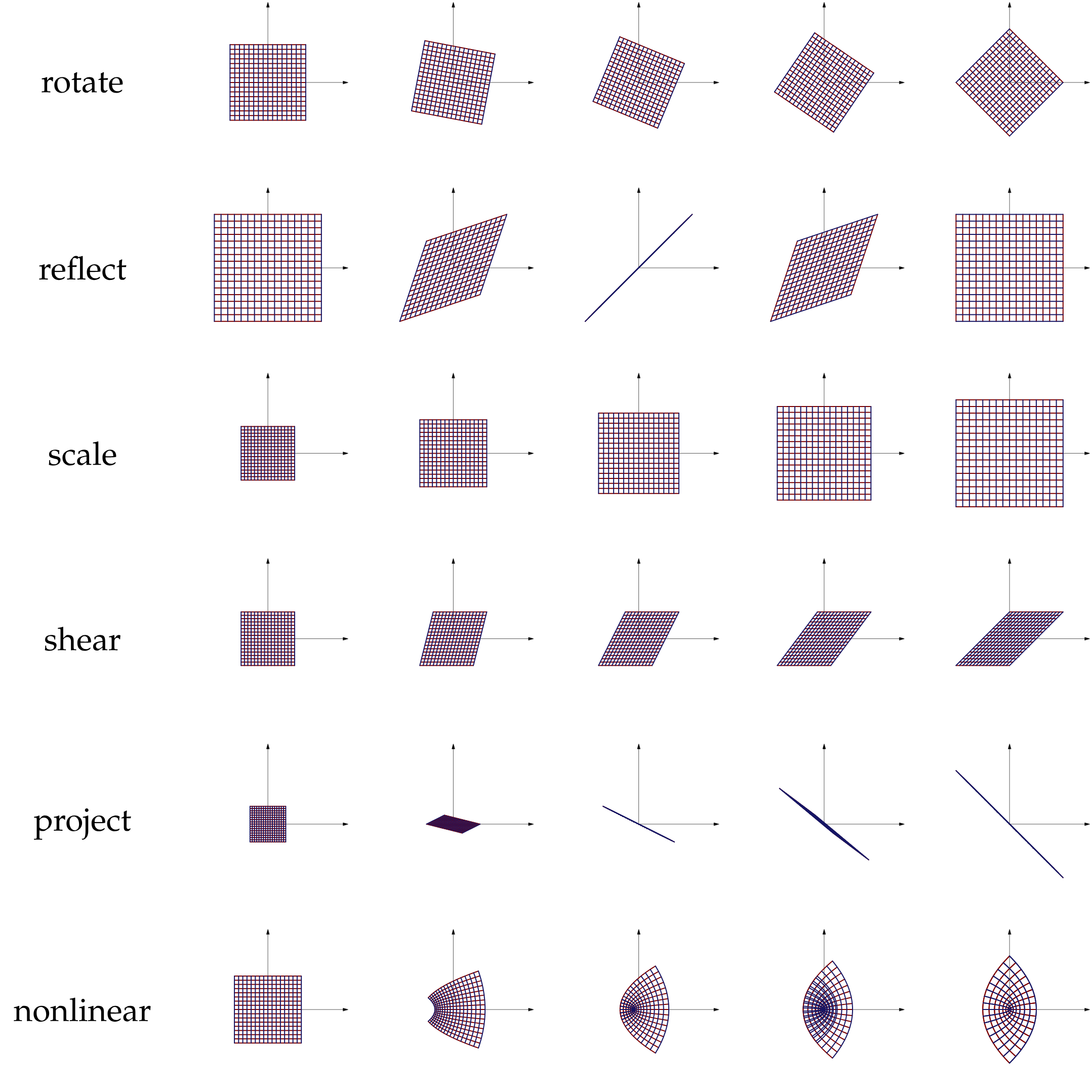
In fact, Matrix Multiplication is a form of matrix transformation that can be characterized as a linear transformation, once it transforms a matrix from ${\mathbf{R}}^n\to {\mathbf{R}}^{\mathbf{m}}$ linearly, and the function can be thought as the second multiplied matrix.

---

How does it work?

A linear transformation $T:X\to W$can be mathematically written as:

$$\begin{array}{rl}& T:{\mathbf{R}}^n\to {\mathbf{R}}^m\\ & T(x_1,x_2,\dots ,x_n)=(w_1,w_2,\dots w_m)\end{array}$$

Where $T$ is a function which transform any vector $x\in {\mathbf{R}}^n$ to $w\in {\mathbf{R}}^m$, given that it satisfies the following properties:

$$\begin{array}{rl}& T(x+y)=T(x)+T(y)\\ & \text{and}\\ & T(ax)=aT(x)\end{array}$$

For transformations which do not satisfy the above conditions, it’s not characterized as a linear transformation.

---

Kernel and images of linear transformations

We can define the kernel of a linear transformation $T:\mathbf{V}\to \mathbf{W}$, as the vectors in the vector space $W$, which when the function $T$ was applied, resulted in a zero vector.

This is can be mathematically written as:

$$ker(T)=\{\mathbf{v}\in \mathbf{V}:T(\mathbf{v})=\vec{0})\}$$

---

The image of a linear transformation $T:\mathbf{V}\to \mathbf{W}$ can be defined as the resultants that are vectors in the vector space $\mathbf{V}$. This is mathematically written as:

$$im(T)=\{T(\mathbf{v}):\mathbf{v}\in \mathbf{V}\}$$

The kernel and image is a subspace of $\mathbf{V}$ and $W$

Given the linear transformation $T:\mathbf{V}\to \mathbf{W}$, both $im(T)$ and $ker(T)$ are subspaces of $\mathbf{W}$ and $\mathbf{V}$, respectively. This is written as $ker(T)\subseteq \mathbf{V}$ and $im(T)\subseteq \mathbf{W}$.