Linear Dependency of Vectors

What is it?

In Linear Algebra, it’s possible to classify different sets of Vectors inside of a vector space as linearly dependent or linearly independent.

Linearly dependent vectors, in a ${\mathbf{R}}^2$ space, would be on the same line, with the same direction.

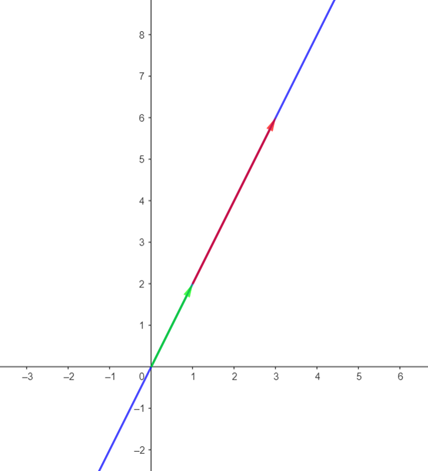
However, linearly independent vectors, in a ${\mathbf{R}}^2$ space, have different directions.

---

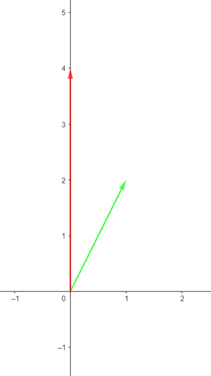
How does it work?

A set of vectors $\{{\mathbf{v}}_1,{\mathbf{v}}_2,\dots {\mathbf{v}}_n\}$ belonging to a vector space $\mathbf{V}$ is said to be linearly dependent, if:

$$\begin{array}{rl}& c_1{\mathbf{v}}_1+c_2{\mathbf{v}}_2+\cdots +c_n{\mathbf{v}}_n=0\\ & \\ & \text{where }{c}_i\text{ are constants and not all are null}\end{array}$$

And the same set is said to be linearly independent, if:

$$\begin{array}{rl}& c_1{\mathbf{v}}_1+c_2{\mathbf{v}}_2+\cdots +c_n{\mathbf{v}}_n=0\\ & \\ & \text{where }{c}_1=c_2=c_n=0\end{array}$$

Writing the above equation will result in a homogeneous system. If the system has only a trivial solution, then the set of vectors is linearly independent, otherwise, not trivial solutions indicate that the set is linearly independent.

For example, given the vectors ${\mathbf{v}}_1=(1,2)$ and ${\mathbf{v}}_2=(2,4)$, we can assume they are linearly dependent because ${\mathbf{v}}_2$ is a multiple of ${\mathbf{v}}_2$. However, we can check this:

$$\begin{array}{rl}& c_1{\mathbf{v}}_1+c_2{\mathbf{v}}_2=0\\ & c_1(1,2)+c_2(2,4)=0\\ & (c_1+2c_1)+(2c_2+4c_2)=0\\ & \\ & \text{which results in}\\ & \{\begin{array}{l}{c}_1+2c_1=0\\ 2c_2+4c_2=0\end{array}\end{array}$$

From the resultant linear system, we can solve it and determine if it is an inconsistent, independent or dependent system, which will then result if it’s linearly independent or dependent*.