Least Squares Method

What is it?

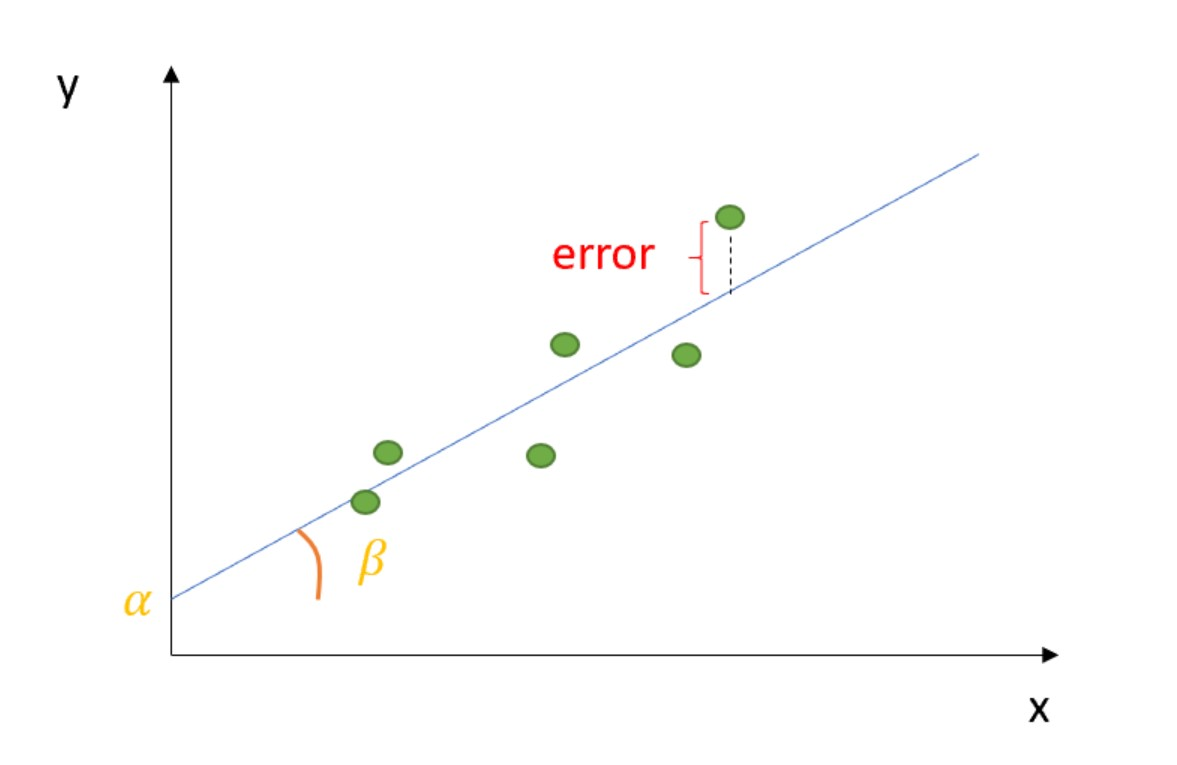
The least squares method is a mathematical method used in Statistics and Machine Learning to find the best-fitting line of a set of data. It’s a method widely used for Linear Regression and other regressive statistical models, to find the relation between variables and estimating outcomes.

The objective is to find a best-fitting line based on the deviation from all measured data points, and the deviation itself is measured with the squared error ${ϵ}^2$.

---

Applying the Least Squares method

We can use Linear Algebra concepts on collected data to find the best-fitting line. Given a set of data, we can map the line function $y=ax+b$ to the known data of $x,y$, and then we would discover the $a,b$ coefficients:

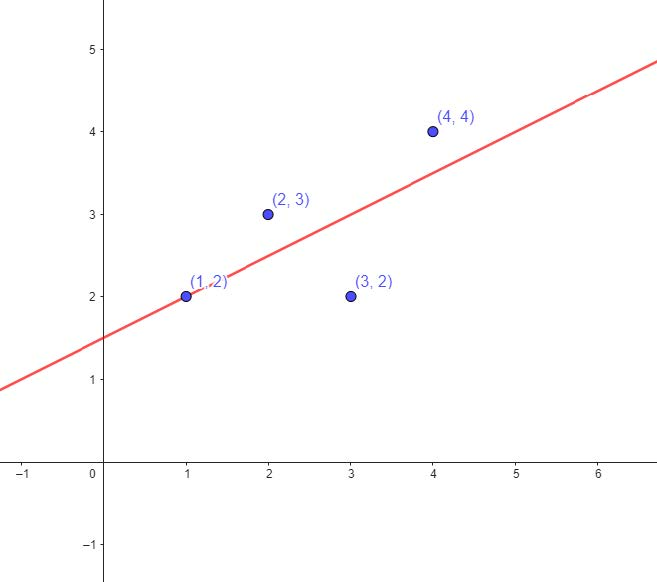
X	Y
1	2
2	3
3	2
4	4

$$\{\begin{array}{l}a+b=2\\ 2a+b=3\\ 3a+b=2\\ 4a+b=4\end{array}\text{rewritten as }A\left(\begin{array}{cc}1& 1\\ 2& 1\\ 3& 1\\ 4& 1\end{array}\right)\ast x\left(\begin{array}{c}a\\ b\end{array}\right)=b\left(\begin{array}{c}2\\ 3\\ 2\\ 4\end{array}\right)$$

Because it’s a overdetermined system, with more equations than unknown variables, we solve $A^{T}Ax=A^{T}b$. Calculating $A^{T}A$ and $A^{T}b$, we can write the equivalent system:

$$\{\begin{array}{l}30a+10b=30\\ 10a+4b=11\end{array}$$

Which then, we can solve using the Gauss-Jordan Elimination Method to conclude that $a=0.53,b=1.43$. Replacing the value of $a,b$ in the original function, we can discover the best-fitting line of $y=0.53x+1.43$, which would result in the following graph: