Mutual Information

What is it?

Mutual Information between two variables describes the extent to which knowledge of one quantity reduces uncertainty about the other. In this case, uncertainty refers to the Entropy of the variables. In other words, if you know the value of a feature, how confident would you be about predicting a target?

It may sound very similar to Correlation, but mutual information is not restricted only to linear relationships. It captures any kind of relationship between variables, being linear or non-linear, and they can be both continuous and discrete variables.

It’s given by the formula:

$$I(X;Y)=\sum _x\sum _{y}P(x,y)\log \left[\frac{P(x,y)}{P(x)P(y)}\right]$$

Given two discrete variables $X,Y$, with its respective probabilities $P(x),P(y)$ and joint probability $P(x,y)$.

---

Mutual Information and Entropy

One might think that the formula above looks very similar to the formula of Entropy, and they indeed are! Mutual information is the uncertainty, or entropy, common to both $X$ and $Y$, being possible to represent the entropic quantities using set theory.

And one could derive the formulas too:

$$\begin{array}{rl}& I(X;Y)=\sum _x\sum _{y}P(x,y)\log \left[\frac{P(x,y)}{P(x)P(y)}\right]\\ & \\ & \text{could be written as}\\ & \\ & I(X;Y)=H(X)+H(Y)-H(X,Y)\end{array}$$

---

How does it work?

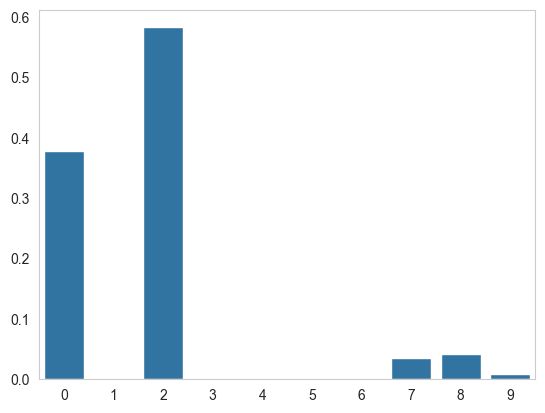
We can easily calculate the mutual information of a feature and its target using scikit-learn, for both real-value and categorical targets. For continuous features, use mutual_info_regression, and for categorical features, mutual_info_classif.

from sklearn.datasets import make_classification  
from sklearn.feature_selection import mutual_info_regression  
  
X, y = make_classification(n_features=10, n_informative=2, random_state=42)  
  
plt.grid(False)  
sns.barplot(mutual_info_regression(X,y));

Which will return the mutual information of each feature:

---

References

• Entropy and mutual information - Information Theory lecture - Tufts University.