What is it?
Dimensionality reduction is the process of decreasing the amount of features in a Machine Learning problem. Normally, one would think the more data, the merrier, but when this data reaches the millions of features that may or not be important to the algorithm, a good idea is to keep only the valuable features, that can give the best information about the problem.
Another issue that dimensionality reduction can help, is slow training times. Having too many features with some specifics algorithms can lead to ridiculously slow training. One could also reduce the features to improve training times.

About dimensionality, yeah, it’s the geometry dimension concept, meaning it’s possible to have those unfathomably high dimensions that scare the human brain. In other words, it also works great with data visualization, making it possible to render comprehensible visualizations of higher-dimensions data, like seen above.
How does it work?
The goal of dimensionality reduction is not to just discard features, but actually trim the data so only the relevant ones stay. But because of the nature of higher dimensions, training data becomes very sparse with high-dimensional spaces, causing issues for the performance of algorithms, specially for distance-based ones, like Linear Regression. This is called the Curse of Dimensionality.
The curse of dimensionality
The expression, brought first by Richard E. Bellman, refers to the issues that arise when dealing with high-dimensional spaces.
The general issue is that when dimensionality increases, the volume of space increases so fast that the current available data become sparse, and then the data necessary to obtain a reliable result will grow exponentially.
Also, organizing data becomes very messy and slow, because of the space between valuable data points. Another issue is the ratio of signal (valuable data) and noise (irrelevant data) that normally results in a lot of noise for high dimensions. So, in a Machine Learning context, how do we solve this problem?
Dimensionality reduction methods
There are basically two main approaches to reduce dimensionality: projection and Manifold Learning.
Projection
Because in most real-world problems, data is not spread uniformly, it was empirically observed that all data points lie close to a much lower-dimensional subspace. The idea is to project the data into this subspace, which would result in similar distribution, but lower dimensionality.
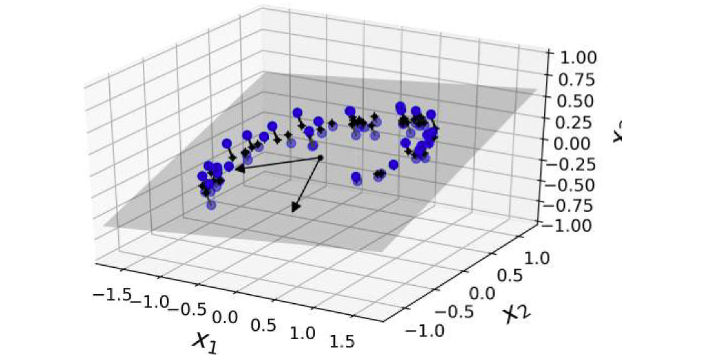
For example, here the hyperplane of a 3D space was found taking into account the distance of it and all data points.
Manifold Learning
There are instances where projecting data to a lower-dimension may not represent the information of the original data. In these cases, the subspace can twist, turn and roll around. For example, in the Swiss Roll dataset:

Manifold Learning remedies this situation. Instead of just projecting to a lower dimension, it assumes that the data lie close to a lower-dimensional manifold and that the model will benefit from a dimensionality reduction. So, always train the model before, so you can have a solid baseline.
Algorithms
The two most popular algorithms are:
- PCA for linear problems
- Kernel PCA for non-linear problems.
Some Manifold Learning popular algorithms are: