Riemann Sum

What is it?

The Riemann Sum, named after Bernhard Riemann, is a method for approximating areas under a curve or any general shape that can be simplified using rectangles, using only the sum of said rectangles. These rectangles can follow an equal width rule or not.

Riemann Sum is one of the building blocks of Integration, even though it can be done without involving Calculus at all. When used to sum rectangles with infinitesimally widths, it behaves the same as Integrals.

Approximating Areas

The main principle is to draw rectangles that follow the shape of a curve, and then calculate the sum of areas. This is used to give an estimate of the actual area.

But then, one could increase the number of rectangles with the objective of minimizing the errors, that could over-estimate or under-estimate. This increase in rectangles can be ad infinitum, until it reaches a satisfying solution.

---

Types of approximation

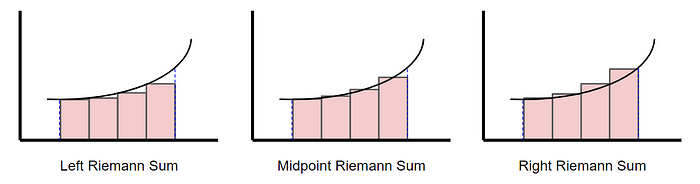
There are three ways to perform a Riemann Sum, left, right and midpoint sum. These will determine the height of the rectangles, also influencing if the end result is over-estimated or under-estimated.

Using the left point rule, the height of each rectangle is determined by where the upper left corner touches the curve.

Using the midpoint rule, the height is determined where the middle of the rectangle touches the curve.

Whereas in the right point rule, the height is determined by where the upper right corner touches the curve.

---

How does it work

You can approximate the area under a curve between an interval $[a,b]$, using the following steps:

• Get the subintervals and rectangle width

Divide the interval length between the number of subdivisions/ rectangles $x_n$ , resulting in the subintervals length/ width of rectangles, $\Delta x$ .

$$\Delta x=\frac{b-a}{n}$$

Given any subdivision $[a,b]$, the first subinterval is $[x_1,x_2]$; the second is $[x_1,x_2]$, the $i^{th}$ interval is $[x_i,x_{i+1}]$.

• Get the height of the rectangle

Here, we apply the above point rules to determine the height of each rectangle. Given a random selected rectangle $x_i$ :

Rule	Equation
Left point	$f(x_i)$
Mid point	$f(\frac{x_1+x_{i+1}}{2})$
Right point	$f(x_{i+1})$

• Calculate the area

Apply the sum of each rectangle area, given by the notation:

$$\sum _{i=1}^{x_n}f(x_i)\ast \Delta x$$