What is it?

Differentiation is a fundamental of Calculus which studies rates of change and slopes of curves. It allows determining how a function’s output changes when its input changes ever so slightly.

Basically, differentiation is the process of finding the derivative of a function.

Differentiation rules

Derivatives are used to define the rate of change and instantaneous slope at a given point. But using the definitions takes too much time, so there are some rules that help to find the derivatives of a function.

These are some of the most commonly used rules. To see a list containing all of them, click here.

Polynomial and exponential functions

Let’s start with the most basic ones, some simple polynomial functions, power functions and exponential functions.

Constant function

The easiest of all functions, the constant function, is given by the general form $f (x) = c$ , meaning that $y = c$ . It gives a straight line in a graph, with slope equal to 0, resulting in a derivative o $f^{'} (x) = 0$ .

f^{'} (x) = h \to 0 lim \frac{f ( x + h ) - f ( x )}{h} = h \to 0 lim \frac{c - c}{h} = h \to 0 lim 0 = 0

Power function

Functions of the general form $f (x) = x^{n}$ , where $n$ is a positive integer, are power functions. If $n = 1$ , then $f (x) = x$ , which would result in $f^{'} (x) = 1$ . If $n \neq = 1$ , we can use the Power Rule, which states:

f^{'} (x^{n}) = n x^{n - 1}, x \in R

This is a general case, which can be proven using the definition:

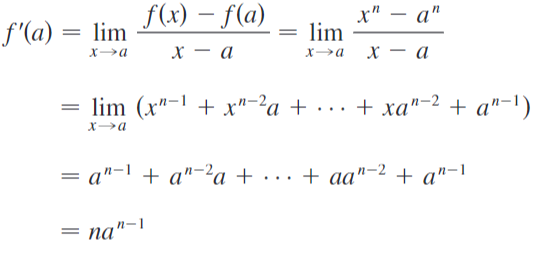
Exponential functions

Exponential derivatives are a very specific. One of the popular forms of an exponential function is $f (x) = e^{x}$ , where $e$ is the Euler’s number, which is its own derivative. For details, check out this link.

For functions that follow the general form $f (x) = a^{x}$ , the derivative of an exponential function is the product of the exponential function $a^{x}$ and $ln a$ , that is:

f^{'} (a^{x}) = a^{x} ln a, a > 0

Derivatives between functions

When there are functions in a sum and subtraction between itself, or multiplication by a constant, the derivatives of the result can be calculated using the old functions.

Multiplication by constant

The Constant Multiplication Rule states that the derivative of a constant times a function is the constant times the derivative of the function.

f^{'} (c * x) = c [f^{'} (x)], or \frac{d}{d x} [c f (x)] = c \frac{d}{d x} f (x)

Sum and substraction of functions

The Sum Rule states that the derivative of a sum of functions is the sum of derivatives. This allows easier calculations when this rule is appliable.

(f (x) + g (x))^{'} = f (x)^{'} + g (x)^{'}

The Difference Rule is similar, but works with subtraction instead of addition.

(f (x) - g (x))^{'} = f (x)^{'} = g (x)^{'}

Product and quotient of functions

The Product Rule states that the derivative of a product of two functions is the first function times the derivative of the second functions plus the second functions times the derivative of the first function.

(f (x) * g (x))^{'} = f (x) * g (x)^{'} + g (x) * f (x)^{'} or (f g)^{'} = f g^{'} + g f^{'}

The Quotient Rule looks it not as similar to the product rule like sum and subtraction. It states that the derivative of a quotient is the denominator times the derivative of the numerator minus the numerator times the derivative of the denominator, all divided by the square of the denominator, which translates to:

(\frac{f}{g})^{'} = \frac{g f ^{'} - f g ^{'}}{g ^{2}}

Chain Rule

The Chain Rule is all about composite functions, so functions that depends on the values of other functions. It states that the derivative of a composite function $F (x) = f (g (x))$ is given by:

F^{'} (x) = f^{'} (g (x)) * g^{'} (x)

References

James Stewart’s “Calculus - Early Transcendentals” — Section 3.1, p. 171.
Derivative of Exponential Function — Cuemath — Blog post.

🍁Lucas' Garden

Explorer

Differentiation