Integrals

What is it?

An Integral is the main mathematical concept in Integration, having the same relationship as Derivatives being the operation of Differentiation. Integrals are heavily used in analytical geometry and Machine Learning for metrics like ROC-AUC.

An integral is the reverse of a derivative. In fact, the process of finding the anti-derivative of a function is called Integration. In other words, if you have a derivative $f^{\prime }(x)$, the original function $f(x)$ is our anti-derivative, also called integrals.

You can interpret an integral as a continuous sum of infinitesimally small numbers, used to calculate curved areas and volumes. An integral is the representation of the area under a curve of a function. For example, an integral could be used to calculate the area $A(x)$ below:

---

Notation and Definition

The exact definition of a integral is the function of the area bounded by a curve, the x-axis and two points that limit the area.

So, given a function $f$ defined for $a\le x\le b$, we can divide the interval $[a,b]$ into infinite $n$ sub-intervals of width $\Delta x=\frac{(b-a)}{n}$. Taking $x{}_i{}^{\ast }$ as any sample point in the sub-intervals, the definite integral of $f$ from $a$ to $b$ is:

$$\begin{array}{rl}& {\int }_a^{b}f(x)dx=\underset{n\to \infty }{\lim }\sum _{i=1}^{n}f(x{}_i{}^{\ast })\Delta x\\ & \\ & \text{where}\\ & \\ & \Delta x=\frac{b-a}{b}\text{and}{x}_i=a+i\Delta x\end{array}$$

The symbol $\int$ was introduced by Leibniz, and is called the integral sign. The elongated S represents the limit of sums. In the notation above, $f(x)$ is called the integrand, which is the function to integrate. The points $a$ and $b$ are the limits of integration. $dx$ implies that the independent variable which will be “sliced” is $x$

---

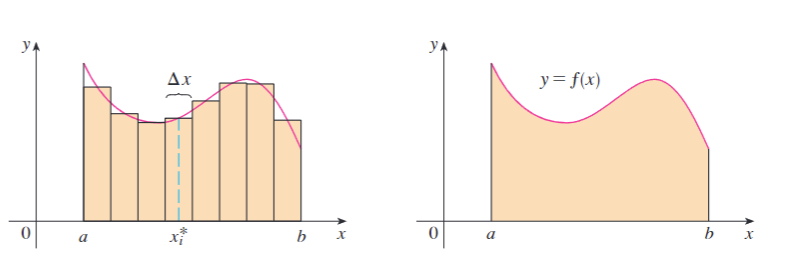
Finding the approximate area

To find the approximate area under the curve, like the image above, one could use rectangles that follow the shape of the curve to estimate the value of the area.

This method is called Riemann Sum, which consists of any approximating sum made up of rectangles of equal or unequal width. You may use this method if Integration proves to be overkill for the context.

Finding the exact area

To find the exact area under a curve, one could just apply a limit to an existing Riemann Sum. Well, actually, an integral is the limit of a Riemann Sum when the width of rectangles tends to zero and the number of rectangles tends to infinity. This gives us the definite integral:

$${\int }_a^{b}f(x)dx=\underset{n\to \infty }{\lim }\sum _{i=1}^n\begin{array}{c}\left[f(x_i)\ast \frac{b-a}{n}\right]\end{array}$$

Let’s start with an example. Given a function $f(x)=x+1$, we can calculate the integral, using the same rules used in Differentiation:

$$\int (x+1)=\frac{x^2}{2}+x+C$$

The C constant

For indefinite integrals, we insert the $C$ constant in any integral, to account any constant in the original function that could not be retrieved.

---

Definite and indefinite integral

An integral is definite if the lower and upper limit of the area to be calculated is also defined. If no limits are specified, the integral can be considered indefinite.

$$\begin{array}{rl}& \int (x)dx\text{is indefinite. No limits defined.}\\ & {\int }_0^2(x)dx\text{is definite. Defined limits.}\end{array}$$

The methods to integrate a function is the same for both definite and indefinite integrals. However, a additional last step is required for definite integrals.

---

Indefinite integrals

Indefinite integrals don’t specify limits to the integration. That way, it appeals to a more general integration of a function, instead of integrating to specific points.

Given a function $f(x)=x+1$, one could integrate it, resulting in $\int (x+1)dx=\frac{x^2}{2}+x$, and that’s already known. But now, we should also add $C$ to the result. $C$ represents any independent variable from the original function, which we can’t retrieve its exact value, so we use $C$ as a placeholder.

---

Definite integrals

Different from indefinite integrals, now we have specified limits to integrate upon. Because we have a defined area in our function, we can now calculate the area under the function.

Before, we stopped at $\int (x+1)dx=\frac{x^2}{2}+x$. But when we insert the limit into the integral, we can evaluate the definite integral. We will evaluate the result with $x$ as the upper and lower limit and get the difference between them. This would result in the area.

$$\begin{array}{rl}& {\int }_0^2(x+1)dx=\frac{x^2}{2}+x\\ & \text{AUC}=(\frac{0^2}{2}+0)-(\frac{2^2}{2}+2)\\ & \text{AUC}=0-4\\ & \text{AUC}=4\text{square units}\end{array}$$

---

Reference

• An Integrals Crash Course — Medium.

• James Stewart’s “Calculus - Early Transcendentals” — Section 5, p. 354.