Ruffini's Rule

Described in 1809, by the Italian mathematician Paolo Ruffini, the Ruffini’s Rule is a method for division of polynomials. It can also be used for finding the roots of a polynomial.

---

Finding the root of a cubic polynomial

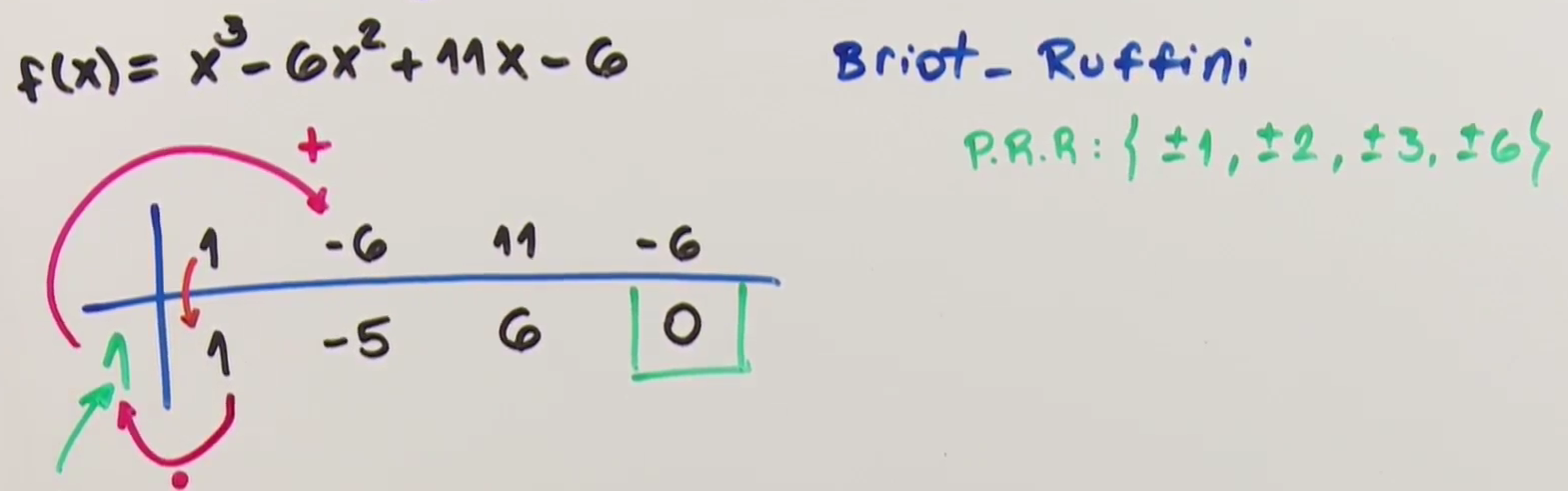
One could use the Ruffini’s rule to lower the degree of a polynomial until it becomes easier to solve, while also discovering the roots. Given an equation:

$$p(x)=x^3-6x^2+11x-6$$

One could guesstimate one root using the Rational Root Theorem and probable real roots:

1. Find the independent term, and in this case would be $-6$. Then, its factors — the values which divide the term evenly — would be $[\pm 1,\pm 2,\pm 3]$.

2. Apply the Ruffini’s Rule to each of the factors until one of them results in 0.

3. When one results in 0, that factor is a root.

4. Then you can get the remainder, and work your way to find other roots! In this case the remainder would be $x^2-5x+6$.

---